МАЛЫЙ МЕХМАТ МГУ

Лекция 1 (151) 7.10.2006.

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Бросание монеты

Лемма об отражении позволяет найти величины многих вероятностей, связанных с бросанием монеты; в частности, вероятность того, что впервые количество орлов и решек сравняются после ровно 2n бросков.

Подробно об этом рассказано во «Введении в теорию вероятностей и её приложения» В. Феллера. Начальные сведения о теории вероятностей можно узнать из книги «Основные понятия теории вероятностей» А.Я. Хинчина.

Лекция 2 (152) 14.10.2006.

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», учитель школ №№ 1018 и 1543.

Задача М1000 задачника «Кванта»

Николай Борисович Васильев под «круглым» номером 1000 включил в задачник «Кванта» следующую задачу Архимеда. Пусть треугольник ABC вписан в окружность, причём AB < BC; M — середина дуги AC, расположенная с той же стороны от прямой AC, что и точка B. Докажите, что основание P перпендикуляра, опущенного на отрезок BC из точки M, делит ломаную ABC пополам, то есть AB + BP = PC.

Девятикласница Эмма Акопян придумала следующее удивительно короткое решение задачи Архимеда. В силу теоремы о вписанном угле величины углов BAM и BCM, опирающихся на одну и ту же дугу BM, равны. Поэтому при повороте треугольника ABM вокруг точки M, при котором точка A переходит в точку C, треугольник ABM переходит в некоторый треугольник CDM, где точка D лежит на отрезке MC. При этом MB = MD. Поскольку высота равнобедренного треугольника является и его медианой, то BP = PD, что и требовалось доказать.

Кроме задачи Архимеда, на лекции была разобрана следующая задача. Через фокус F эллипса проведём любую его хорду AB, построим касательные в концах этой хорды и найдём точку I пересечения этих касательных. Оказывается, отрезки IF и AB перпендикулярны.

Доказательство использует оптическое свойство эллипса: если G — другой фокус эллипса, то AI и BI — биссектрисы внешних углов A и B треугольника ABG. Поэтому I — центр вневписанной окружности треугольника ABG. Основание P перпендикуляра, опущенного из центра вневписанной окружности на отрезок AB, делит периметр треугольника ABG пополам, то есть PA + AG = PB + BG. Осталось заметить, что FA + AG = 2a = FB + BG, где a — большая полуось эллипса.

Аналогичное утверждение верно и для параболы, и для гиперболы (для гиперболы роль центра вневписанной окружности играет центр вписанной окружности).

Лекция 3 (153) 21.10.2006.

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», учитель школ №№ 1018 и 1543.

Аксиома выбора и вполне упорядоченные множества

Аксиома выбора гласит: для любого множества M существует функция f, определённая на множестве всех непустых подмножеств множества M и такая, что любое её значение f (A), где A К, является элементом множества A.

Принцип максимальности Хаусдфорфа гласит: всякое линейно упорядоченное подмножество частично упорядоченного множества содержится в некотором максимально возможном линейно упорядоченном подмножестве этого частично упорядоченного множества.

Лемма Цорна: если всякое линейно упорядоченное подмножество частично упорядоченного множества ограничено сверху, то в M существует максимальный элемент.

Теорема Цермело о полном упорядочении: всякое множество можно вполне упорядочить, то есть превратить в линейно упорядоченное множество, всякое непустое подмножество которого имеет минимальный элемент.

Аксиома выбора, принцип максимальности Хаусдорфа, лемма Цорна и теорема Цермело равносильны между собой.

Лекция 4 (154) 28.10.2006.

Владимир Николаевич ЧУБАРИКОВ,

исполняющий обязанности декана механико-математического факультета МГУ имени М.В. Ломоносова, профессор кафедры математического анализа, лауреат премии имени М.В. Ломоносова за педагогическую деятельность 1999 года, автор более 100 научных работ и 8 книг.

Математика в Московском университете

В выступлении будут затронуты исторические аспекты развития математики в Московком университете, основные тенденции современной математической науки и некоторые её проблемы. Лекция была составной частью фестиваля науки МГУ.

Лекция 5 (155) 11.11.2006.

Михаил Викторович ИГНАТЬЕВ,

студент Самарского университета, учитель гимназии №2, победитель конкурса педагогических проектов компании Intel с проектом «Праздник непослушания на уроке геометрии» (в соавторстве с И.К. Баталиной)

Квантовая алгебра

Часто говорят: квантовая физика, квантовый компьютер, квантовые вычисления... Но что такое квантование с точки зрения математики?

Квантовый аналог (или q-аналог) математического объекта A — это набор объектов A_q, зависящий от параметра q и стремящийся к А при стремлении q к 1. Эту несколько размытую идею наполняют смыслом конкретные задачи и конструкции. Например, квантовый аналог натурального числа n — это сумма первых n членов геометрической прогрессии с первым членом 1 и знаменателем q.

Будут рассмотрены аналогично введённые квантовые факториалы, квантовые числа сочетаний, квантовый треугольник Паскаля, квантовый бином Ньютона, квантовые производные. При изучении квантового бинома Ньютона обнаружится, что удобно рассматривать переменные, связанные некоммутативным умножением: xy = qyx. В этом состоит вторая основная идея квантовой алгебры: квантование — это переход от коммутативных объектов к некоммутативным.

С материалом этой лекции можно познакомиться по книге В.Г. Каца и П. Чена «Квантовый анализ» (издательство МЦНМО, 2005 год).

Лекция 6 (156) 18.11.2006.

Николай Николаевич ОСИПОВ,

доктор физико-математических наук, профессор кафедры прикладной математики Красноярского государственного технического университета и кафедры алгебры Красноярского государственного педагогического университета

Кубатурные формулы, точные на многочленах

Для приближённого вычисления интегралов используют кубатурные формулы. Было расказано об общих принципах конструирования таких формул, особенно о формуле, предложенной Коробовым в 1957 году.

Лекция 7 (157) 25.11.2006.

Александр Васильевич СПИВАК,

учитель школ 1018 и 1543

Тождества и многочлены

Для любого многочлена f через Δf обозначим многочлен, заданный формулой Δf (x) = f (x + 1) – f (x). Очевидно, степень многочлена Δf на единицу меньше степени многочлена f, а старший коэффициент многочлена Δf равен произведению степени многочлена f на старший коэффициент этого многочлена. Была выведена формула для n–кратного применения операции Δ и связанные с этим тождества. Подробно познакомиться с этим можно по статье Николая Борисовича Васильева (опубликованной под псевдонимом В. Вагутен в «Кванте» номер 2 за 1973 год) «Числа C_n^k, многочлены, последовательности». Далее на лекции были доказаны интерполяционная формула Лагранжа и интерполяционная формула Ньютона.

Лекция 8 (158) 2.12.2006.

Александр Васильевич СПИВАК,

учитель школ 1018 и 1543

Числа Стирлинга

Для любого натуральных чисел n и k числом Стирлинга первого рода из n по k называют количество перестановок множества, состоящего из n элементов, в разложении которых на непересекающиеся циклы имеется ровно k циклов. Числом Стирлинга второго рода из n по k называют количество способов разбить n–элементное множество на k непустых подмножеств. Были доказаны рекуррентные формулы и выявлена связь чисел Стирлинга с алгеброй.

Лекция 9 (159) 9.12.2006.

Николай Николаевич СМИРНОВ,

автор более 200 научных работ, в том числе 8 книг. Лауреат премии имени И.И. Шувалова. Член редколлегии международных журналов «Combustion and Flame», «Acta Astronautica», заместитель председателя научного Совета по горению и взрыву при Президиуме РАН, член комитета по микрогравитации Международной астронавтической федерации, член Международного института горения, член Совета №6 по экологии Российского космического агентства, член–корреспондент Международной академии астронавтики, координатор международных проектов по проблемам взрывобезопасности и повышения эффективности добычи жидких полезных ископаемых.

Модели механики и окружающий мир

В занимательной форме с демонстрацией слайдов, мультфильмов и экспериментов будет рассказано о применении моделей и методов механики при решении разноплановых практических задач:

• Волновые процессы в деформируемых твердых, жидких и газообразных средах.
• Образование и эволюция космического мусора.
• Повышение нефтеотдачи нефтеносных пластов.
• Математическое моделирование автотранспортных потоков и вызываемого ими загрязнения атмосферы.
• Разрушение повреждаемых сред.
• Вход тел с большими скоростями в атмосферу.
• Волны в метастабильных системах.
• Переход горения в детонацию в газах;
• Турбулентное горение гетерогенных полидисперсных смесей.
• Динамика гибких связей.

Лекция 10 (160) 16.12.2006.

Вячеслав Дмитриевич КОТЁЛКИН,

кандидат физико–математических наук, доцент кафедры аэромеханики и газовой динамики механико–математического факультета МГУ имени М.В. Ломоносова, ведущий научный сотрудник Института океанологии имени П.П. Ширшова РАН.

Современные представления об эволюции планет и результаты численного моделирования эволюции Земли

Будут представлены сведения: о циклическом характере эволюции Земли (слайды геологических реконструкций суперконтинетов), геохимические данные об эпизодическом характере обмена веществом между верхней и нижней мантиями Земли. Обсуждены понятия термической конвекции и тектоники плит, противоречие между геофизическими и геохимическими данными. Рассматривается эндотермический фазовый переход, открытие перемежающейся конвекции и снятие противоречия. Отмечается российский приоритет в вопросах дифференциации вещества на границе ядро–мантия и химико–концентрационной конвекции. Представлены также тектоника плюмов, следы мелового суперплюма, успехи сейсмотомографии, эклогитизация погружающегося вещества, японская парадигма мантийной конвекции. Приводятся новые сведения о быстрой и горячей аккреции планет. Затронута общая теория эволюции планет В.П. Мясникова и оболочечный закон эволюции. Отмечены актуальные вопросы: природа циклов Вилсона, особенности корообразования, асимметрия Земли. Даются представления о математических моделях и численном моделировании. Объясняется термохимическая модель Лобковского–Котёлкина, по которой проведено моделирование, и демонстрируются фильмы, визуализирующие численные эксперименты по эволюции Земли. Описывается открытие глобальных мантийных переворотов–овертонов, пространственная конфигурация овертонов, и их вырождение в региональные аваланши. Проводится сопоставление численных результатов с фактическими данными по Земле, обсуждение и анализ результатов.

Это вторая лекция из цикла «Беседы о механике» — последняя в 2006 году. Возобновится лекторий 10 февраля 2007 года.

Лекция 11 (161) 10.2.2007.

Алексей Валериевич ЗАБРОДИН,

заведующий кафедрой вычислительной механики механико-математического факультетата МГУ, доктор физико–математических наук, профессор, член–корреспондент РАН, лауреат Государственной премии Российской Федерации.

Вычислительная механика — что это такое?

Лекция была запланирована на 16 декабря 2006 года, но не состоялась вследствие болезни лектора.

В занимательной форме с демонстрацией слайдов будут обсуждены следующие актуальные вопросы.

• Сочетание классической механики и современных возможностей решения прикладных задач при использовании супер–ЭВМ. Новые возможности научных исследований, доведение их до численных результатов.
• Дискретизация непрерывных явлений и образов. Язык вычислений (сетки).
• Вычислительные модели — способы математического описания и формулирования решаемых задач на языках вычислительных средств.
• Актуальные задачи вычислительной механики:
  • аэродинамические приложения,
  • геофизические задачи нефтедобычи,
  • ядерно–физические задачи воспроизводства энергии,
  • задачи математической биологии (расшифровка структуры макромолекул).
• Потребные объёмы вычислений при решении прикладных задач. Требования к производительности и памяти вычислительных средств.
• Создание многопроцессорных вычислительных систем — единственный на сегодня путь получения необходимых параметров супер-ЭВМ.
• Представление результатов вычислительных исследований.

Лекция 12 (162) 17.02.2007.

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», учитель школ №№ 1018 и 1543.

Формула крюков

Явная формула для чисел Каталана является частным случаем открытой в 1954 году формулы крюков. Довольно долго были известны лишь сложные доказательства, недоступные школьнику. Недавно выяснилось, что при помощи антисимметрических многочленов можно доказать формулу крюков весьма естественным и простым способом.

Лекция 13 (163) 24.02.2007.

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», учитель школ №№ 1018 и 1543.

Формулы обращения Мёбиуса

Функция Эйлера и многие другие арифметические функции тесно связаны с функцией Мёбиуса и формулами обращения Мёбисуса. Например, при помощи одной из формул обращения можно найти вероятность того, что случайно выбранная правильная дробь несократима.

Лекция 14 (164) 3.03.2007.

Андрей Михайлович РАЙГОРОДСКИЙ,

доктор физико-математических наук, доцент кафедры математической статистики механико-математического факультета МГУ.

Числа Рамсея

Многие знают, что среди любых шести человек есть трое знакомых друг с другом или трое незнакомых между собой. Этот результат связан с большой и многогранной наукой, которая называется теорией Рамсея. Будет рассказано о нескольких классических вопросах этой теории и об идеях, с помощью которых на эти вопросы были даны ответы. Например, интересно знать, каково для данных натуральных чисел s и t такое минимальное натуральное число R, что среди любых R человек заведомо есть либо s знакомых друг с другом, либо t незнакомых. Несмотря на свою исключительную популярность, эта задача далека от решения. Достаточно заметить, что даже значения R(4,5) никто не знает.

Лекция 15 (165) 10.03.2007.

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», учитель школ №№ 1018 и 1543.

Крылатый квадрат

Теорема Ферма–Эйлера гласит: всякое простое число, дающее остаток 1 при делении на 4, представимо в виде суммы квадратов двух целых чисел. Известно несколько разнообразных доказательств. Одно из них использует теорему Вильсона о том, что для любого простого числа p факториал числа p – 2 даёт остаток 1 при делении на p, а также единственность разложения целого гауссова числа в произведение простых гауссовых чисел, другое — принадлежащее Жозефу Луи Лагранжу — использует теорему Вильсона и принцип Дирихле. Есть и другие остроумные доказательства.

Дон Цагир придумал доказательство, изумляющее своей неожиданностью. Начинается оно с того, что если простое число p нечётно и представимо в виде суммы двух квадратов, то одно из слагаемых нечётно, а другое чётно. Поэтому он рассматривает уравнение p = x² + 4y². Далее он записывает последнее уравнение в виде системы: p = x² + 4yz и y = z. Казалось бы, ничего не изменилось. Но далее он рассматривает только первое уравнение системы и замечает, что вместе с каждой удовлетворяющей ему тройкой (x; y; z) существует тройка (x; z; y), вследствие коммутативности умножения тоже удовлетворяющая этому уравнению. Таким образом, решения первого уравнения системы, не удовлетворяющие второму её уравнению, разбиваются на пары. Доказав при помощи устрашающе выглядящей алгебраической конструкции, что количество решений первого уравнения нечётно, Дон Цагир завершает доказательство. По-русски его можно прочитать в статье «Теорема Ферма–Эйлера о двух квадратах» В.М. Тихомирова в десятом номере журнала Квант за 1991 год (страницы 9, 10, 11 и 12), по-английски — в оригинальной статье в журнале American Mathematical Monthly (том 97, 1990 год, страница 144).

Оказывается, алгебраическая конструкция Цагира не нужна: вместо замысловатых формул и неравенств достаточно изобразить величину x² + 4yz в виде «крылатого квадрата» — квадрата со стороной x и четырёх прямоугольников размером y × z каждый. Таким образом, доказательство Цагира, считавшееся хотя и самым коротким, но малопрозрачным, становится абсолютным шедевром: оно и очень короткое, и самое ясное. Геометрическая конструкция порождает много новых интересных вопросов: например, удивительным образом для большинства первых 10000 простых чисел, дающих остаток 1 при делении на 4, приходится перебирать все без исключения существующие крылатые квадраты, чтобы дойти перестройками Цагира от тройки x = 1, y = 1, z = (p – 1) / 4 до тройки, в которой y = z.

Лекция 16 (166) 17.03.2007.

Павел Анатольевич КРУЧИНИН,

кандидат физико–математических наук, доцент, учёный секретарь кафедры прикладной механики и управления мехмата МГУ;

Степан Степанович ЛЕМАК,

доктор физико–математических наук, ведущий научный сотрудник кафедры прикладной механики и управления мехмата МГУ, лауреат Государственной премии РФ.

Как обмануть организм человека при обучении на тренажёре?

Это четвёртая лекция из цикла лекций о механике. Она посвящена имитации на динамических тренажёрах вождения автомобиля, самолета или космического аппарата. Ощущения тренируемого должны совпадать с ощущениями водителя реального автомобиля или самолета. На первый взгляд это значит, что надо создать такие же воздействия на человека, как и в кабине реальной машины. Однако «полная» модель, описывающая движение автомобиля или самолета, чрезвычайно сложна. К тому же и конструкция тренажера не позволяет воссоздать все особенности воздействий. В связи с этим возникают следующие вопросы.

• Какими органами и что именно воспринимает человек?
• Надо ли отображать движение во всех подробностях, какие воздействия и с какой точностью надо воспроизводить?
• Как управлять тренажёром, чтобы скрыть его конструктивные недостатки?

Лекция 17 (167) 24.03.2007.

Владислав Валерьевич ИЗМОДЕНОВ,

кандидат физико–математических наук, доцент кафедры аэромеханики и газовой динамики мехмата МГУ, заведующий лабораторией Института космических исследований РАН, член редколегии международного научного журнала ASTRA, руководитель международной рабочей группы по исследованию гелиосферы при Международном институте космических исследований (Берн, Швейцария), участник проекта по запуску космического аппарата для исследования границы солнечной системы (запуск намечен на июнь 2008 года), руководитель российских и международных научно-исследовательских проектов по изучению границы Cолнечной системы. Автор более 50 научных работ. Награждён в 2006 году международным комитетом по космическим исследованиям (КОСПАР) медалью имени Я.Б. Зельдовича.

Космическая газовая динамика

Это пятая лекция из цикла лекций о механике. Будет рассказано о бурно развивающейся области науки — космической газовой динамике. Космическая газовая динамика — это наука, в которой движение газовых масс в космических условиях изучается с помощью методов гидроаэромеханики, газовой динамики и магнитной гидродинамики. Космическая газовая динамика часто используется при построении моделей физических явлений, встречающихся в условиях космического пространства. Будет рассказано о роли, которую сыграли аэродинамики в предсказании и объяснении таких астрофизических явлений, как солнечный ветер, кометные хвосты, спиральная структура галактик,... Будут приведены примеры современных исследований, когда с помощью методов газовой динамики были предсказаны явления, обнаруженные впоследствии такими космическими аппаратами, как Хаббл Спейс Телескоп, Вояджер 1 и 2, СОХО, Улис.

Лекция 18 (168) 31.03.2007.

Сергей Валерьевич МАРКЕЛОВ,

выпускник мехмата МГУ, автор задач по геометрии.

Нерешённые проблемы геометрии

Во время Великой Отечественной войны в представлениях к полководческим орденам писали: «Смело и решительно обходя очаги сопротивления, не ввязываясь в затяжные бои, проник далеко вглубь обороны противника.» Так и математика ушла далеко вперёд: в некоторых областях, чтобы понять условия задач, нужно учить лет десять специальный язык сложнее китайского. Прорвавшаяся вперёд наука оставила очаги сопротивления даже в элементарной геометрии: точки, прямые, окружности — условия некоторых интересных понятны даже школьнику, а решать их никто не умеет. Вот несколько таких неподдающихся задач.

• Каково минимальное число цветов, в которые можно так раскрасить плоскость, чтобы концы любого отрезка длины 1 были покрашены в разные цвета?

• Существует ли раскраска точек пространства в 14 цветов, при которой концы любого отрезка длины 1 одного цвета?

• Сколько точек общего положения должно быть отмечено на плоскости, чтобы среди них непременно нашлись вершины выпуклого шестиугольника?

• В любом ли многоугольнике с зеркальными изнутри сторонами можно так разместить лампочку, чтобы он был освещён весь?

• Можно ли несколькими кругами, зеркальными снаружи, не пересекающими друг друга и даже не касающимися, загородить горящую лампочку?

• В любом ли многоугольнике с зеркальными сторонами существует хотя бы один замкнутый путь светового луча?

• Существует ли многоугольник, копиями которого плоскость можно покрыть, но только непериодическим образом?

• Может ли выпуклый многогранник, которым можно замостить всё пространство, иметь больше 38 граней?

• Какова фигура минимальной площади, которой можно покрыть любой многоугольник диаметра 1?

• Какова фигура минимальной площади, которой можно покрыть любую фигуру периметра 1?

• Сколь велика может быть площадь n-угольника диаметра 1 при данном n?

• У любого ли выпуклого многогранника существует развёртка без самопересечений?

• Рассмотрим n точек, не лежащих на одной прямой. Обязательно ли среди них найдётся точка, через которую проходит не менее ⁿ/₃ прямых, соединяющих её с остальными n – 1 точками?

Эта лекция уже была один раз прочитана на лектории МММФ. Но она настолько замечательна и снабжена настолько красивыми мультфильмами, что опять нужна очень и очень многим школьникам. Лектор подготовил и продолжение — рассказ о замощениях плоскости и пространства, содержащий среди прочего и совсем недавние замечательные достижения. Возможно, и такая лекция будет прочитана в этом году.

Лекция 19 (169) 7.04.2007.

Александр Ханевич ШЕНЬ,

кандидат физико-математических наук, старший научный сотрудник Института проблем передачи информации РАН, учитель школы номер 57, автор многих брошюр и книг для школьников и студентов.

Средние значения и вероятности

Сколько раз в среднем нужно бросать кубик, прежде чем выпадет шестёрка? Если мы находимся между двумя лужами на разных расстояниях и движемся случайно в ту и другую сторону, в какой доле случаев мы будем попадать в одну лужу, а в какой в другую? Какова вероятность, что игла данной длины, брошенная на линованную бумагу, пересечёт одну из линий? Такими вопросами занимается теория вероятностей. На многие из них можно ответить при помощи обычного здравого смысла.

Лекция 20 (170) 14.04.2007.

Андрей Николаевич Квашенко,

учитель биологии школы № 1543.

Естественнонаучное драконоведение

Лекция посвящена теоретическому моделированию биосистем (с акцентом на возникновении системных связей в процессе эволюции) на примере эволюции драконов. За отправную точку принимаем информацию, содержащуюся в традиционных мифах и легендах. О драконах было рассказано много совершенно неожиданного.

Лекция 21 (171) 21.04.2007.

Андрей Николаевич Квашенко,

учитель биологии школы № 1543.

Естественнонаучное драконоведение

Это продолжение лекции, прочитанной 14 апреля. Очень советую прийти: всей довольно многочисленной аудитории предыдущая лекция понравилась. Лекция интересна как старшеклассникам, так и младшим школьникам: каждый найдёт что-то своё. Приходите!!!

Лекция 22 (172) 28.04.2007.

МАТИЗЕН Виктор Эдуардович,

кинообозреватель газеты «Новые Известия», глава гильдии киноведов и кинокритиков России, выпускник ФМШ при НГУ, мехмата НГУ и ВГИКа, автор более 1000 публикаций о кино. В 1986 году выпустил книгу «Жизнь шкрабов», во многом основанную на опыте учительской работы. Автор статей «Найдём ошибку» (1980 год, 10 номер журнала «Квант»), «Равногранные и каркасные тетраэдры» (1983 год, 7 номер), «О пользе скатывания шариков» (1980 год, 5 номер), «Перекатывание многогранников» (1989 год, 5 номер), соавтор (с В.Н. Дубровским) статьи «Из геометрии тетраэдра» (1988 год, 9 номер), автор задач 549, 833, 1039, 1067, 1139 «Задачника "Кванта"».

Перекатывания многогранника

Как-то раз на коммунистическом субботнике лектор со своими учениками кантовал тяжёлые каменные обломки. Другой повод — строгая надпись на таре для стеклянных изделий: «НЕ КАНТОВАТЬ!». Лекция посвящена следующим вопросам:

1) что представляет собой множество следов вершин (рёбер, граней) выпуклого многогранника при всевозможных его перекатываниях по плоскости через ребра (из некоторого начального положения)?

2) что такое бесконечно продолженная развертка выпуклого многогранника?

В частности, выясняется, для каких многогранников множество следов его вершин дискретное, а для каких оно заполняет плоскость всюду плотно.

Лекцию сопровождали компьютерные иллюстрации.

Лекция 23 (173) 5.05.2007.

Фёдор Константинович НИЛОВ,

ученик десятого класса лицея «Вторая школа».

Многоугольники, составленные из дуг парабол

Основные определения таковы:

1. Параболическим 2n-угольником называем объединение 2n точек и дуг n парабол, их соединяющих. Его криволинейные стороны — дуги парабол. Для любой из этих парабол существует ровно две противоположные криволинейные стороны, принадлежащие этой параболе. Эти параболы называем образующими. Полным параболическим 2n-угольником называем параболический 2n-угольник, любые две образующие параболы которого пересекаются в 4 точках. Например, вот как выглядит параболический четырёхугольник:
   
2. Параболический многоугольник описанный, если существует окружность, касающаяся его криволинейных сторон в 2n точках.
3. Параболический многоугольник вписанный, если существует окружность, проходящая через все его вершины.
4. Осевая прямая выпуклого четырёхугольника ABCD — прямая EF, проходящая через точку пересечения диагоналей, где E и F находятся на продолжениях противоположных сторон AB и CD соответственно, причём AE : EB = FD : CF.

Основные утверждения таковы:

1. Если парабола и окружность касаются в точках A и B, а точка P лежит на параболе, то расстояние от точки P до прямой AB равно длине касательной, проведённой из точки P к окружности.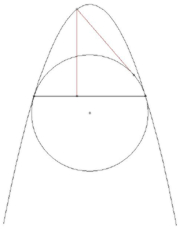
   
2. Параболический четырёхугольник описанный тогда и только тогда, когда его диагонали перпендикулярны.
   
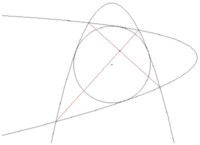
3. Если две параболы пересекаются в двух точках A и B, то окружность, касающаяся этих парабол в четырёх точках, существует тогда и только тогда, когда оси парабол образуют равные углы с прямой АВ.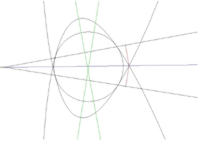
   
4. Параболический четырёхугольник вписанный тогда и только тогда, когда оси парабол перпендикулярны.
   
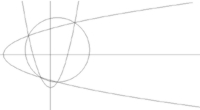
5. Любой параболический четырёхугольник можно перевести аффинным преобразованием во вписанный и описанный параболический четырёхугольник.
6. Если на параболе лежат четыре точки A, B, C и D, то осевая прямая, связанная с ВС и АD, параллельна оси параболы.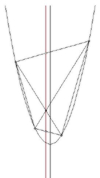
   
7. Диагонали описанного около окружности параболического шестиугольника пересекаются в одной точке.
   
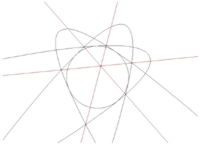
8. Внутри окружности взята точка. Через неё проведены n прямых, которые делят плоскость на равные углы. Рассмотрим параболический 2n-угольник, касающийся окружности в 2n точках. Оказывается, вершины параболического 2n-угольника, образованного этими параболами, принадлежат одной окружности.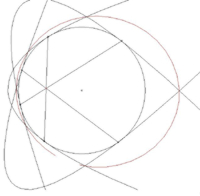
   
9. Если в два параболоида вписана сфера, то точки пересечения этих параболоидов лежат в двух перпендикулярных плоскостях.

Можете ознакомиться с ppt-файлом этой лекции.

Лекция 24 (174) 12.05.2007.

Андрей Николаевич Квашенко,

учитель биологии школы № 1543.

Естественнонаучное драконоведение

Это продолжение лекции, прочитанной 14 и 21 апреля. Интересна как старшеклассникам, так и младшим школьникам: для каждого в ней есть что-то своё.

Лекторий возобновит работу в первую субботу октября 2007 года. Андрей Николаевич Квашенко обещал прочитать подробный курс драконологии (от 10 до 15 лекций) в следующем учебном году.